Previous: The Gelman-King Model

Up: The Gelman-King Model

Next: Application: Calculating Partisan Bias

Generating Hypothetical Elections

Now that the parameters in each election year are estimated, the model can be simulated. For a predictive analysis, the hypothetical vote share in each district is found to be

$$\tilde{v_i} = \tilde{X_i'}\beta + \tilde{\delta} + \tilde{\gamma_i} + \tilde{\varepsilon_i}$$

where $\tilde{X_i'}$ is a (possibly new) vector of predictors corresponding to those terms in $\beta$ . In this case, the two error terms are unidentifiable and once again combine so that

$$\tilde{\gamma_i} + \tilde{\varepsilon_i} \sim N(0,\sigma^2).$$

The $\tilde{\delta}$ term is added under the general uniform partisan swing assumption; that is, for small deviations from the observed outcome, a swing in the overall vote share can be represented as the same swing in each district in the system. This allows the user to investigate two scenarios: what would happen if the average vote were to shift by a small amount, or what the electoral map would look like with a particular average vote share (corresponding to a particular shift in the average vote.)

For an evaluation of an election's underlying properties, or to examine what would happen if we re-ran the election under counterfactual circumstances, we note that the systematic error component $\gamma_i$ can be estimated using the data. Since $y_i$ and $\gamma_i$ are simulated from the bivariate normal distribution,

$$\left[ \begin{array}{c} y_i \\ \gamma_i \end{array} \right] \sim ... ...a \sigma^2 \\ \lambda \sigma^2 & \lambda \sigma^2 \end{array} \right] \right),$$

we can obtain the conditional distribution,

$$\gamma_i\vert y_i \sim N(\lambda(y_i-x_i'\beta),\lambda(1-\lambda)\sigma^2).$$

We then use this estimate of $\gamma_i$ in the simulation equation

$$\tilde{v_i} = \tilde{X_i'}\beta + \tilde{\delta} + \gamma_i + \tilde{\varepsilon_i}.$$

Note that Party 1 wins the election if their share of the two-party vote is greater than one-half. Given $\beta$ and $\gamma$ , we then see that the expected seat share is

$$P(v_i>0.5\vert\beta,\gamma,\delta) = 1-\Phi\left( \frac{0.5-\tilde{X_i'}\beta-\tilde{\delta} + \gamma_i}{\sqrt{(1-\lambda) \sigma^2}} \right).$$

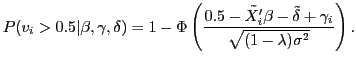
To generate the probability distribution for this quantity, we then draw values for $\beta$ and $\gamma$ given their conditional distributions, and set $\delta$ to its required value given the application.