Previous: Demos and Data Sets

Up: WHATIF: Software for Evaluating

Next: R Function Reference

Technical Details

The computational task of determining the convex hull membership is made feasible even for large numbers of explanatory variables and observations by the solution proposed in King & Zeng (2006), which eliminates the most time-consuming part of the problem: the characterization of the convex hull itself. In addition, they show that the remaining (implicit) point location problem can be expressed as a linear programming exercise, making it possible to take advantage of existing well-developed algorithms designed for other purposes to speed up the computation. Specifically, a counterfactual $x$ is in the convex hull of the explanatory variables $X$ if there exists a feasible solution to the following standard form linear programming problem:

$$C'\eta$$ min 

$$A'\eta=B'$$ s.t.  (1)

$$\eta \geq 0$$

where $C$ is a vector of zeros (so that there is no objective function to minimize); $\eta$ is a vector of coefficients; $A'$ is $X'$ with an additional, final row of $1$ 's; and $B'$ is $x'$ with an additional, final element equal to $1$ .

The default Gower distance (which is suitable for both quantitative and qualitative data) between a pair of $K$ dimensional points $x_i$ and $x_j$ is defined simply as the average absolute distance between the elements of the two points divided by the range of the data:

$$G_{ij} = \frac{1}{K}\sum_{k=1}^K \frac{\left\vert x_{ik} - x_{jk}\right\vert}{r_k}$$ (2)

where the range is $r_k =$   max$(X_{.k}) -$   min$(X_{.k})$ and the min and max functions return the smallest and largest elements respectively in the set including the $k$ th element of the explanatory variables $X$ . The optional squared Euclidian distance (which is suitable only for quantitative data) between points $x_{i}$ and $x_{j}$ is given by the familiar definition, i.e. the sum of the squared differences between the elements of the two points:

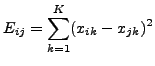$$E_{ij} = \sum_{k=1}^K (x_{ik} - x_{jk})^2$$ (3)